TCLIB Suite
Software-Bibliothek und eigenständige Tools zum Optimieren von telezentrischen Anordnungen
Hauptvorteile
- Modernste Algorithmen für die Verzerrungskalibrierung.
- Mit schnellen und intuitiven eigenständigen Tools wird die beste Fokussierung und Ausrichtung gewährleistet.
- Maximierte Systemleistung für bestmögliche Messergebnisse.
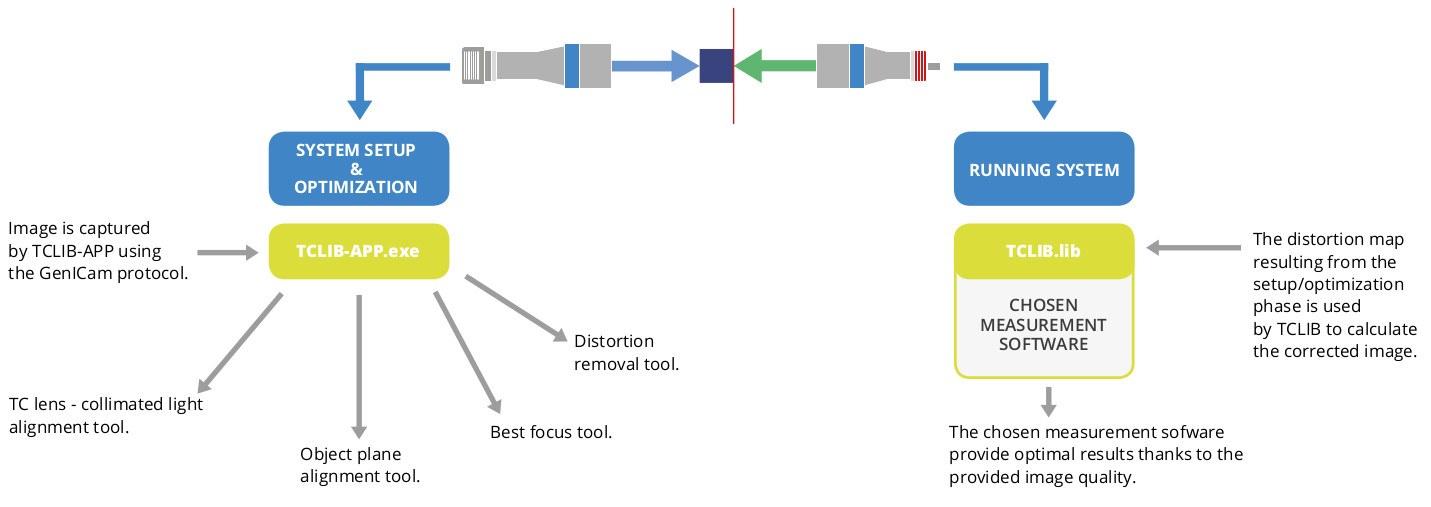
TCLIB Suite ist eine auf C++ basierende Bildverarbeitungssoftware, die zur Optimierung der optischen Leistung einer telezentrischen Anordnung, wie sie in der Regel zu Messzwecken eingesetzt wird, entwickelt wurde. Durch die Verwendung einer .dll-Library und eines speziellen eigenständigen Tools ist es einfach, alle Aspekte einer typischen telezentrischen Anordnung (Fokussierung, Ausrichtung, Verzeichnungskalibrierung) zu berücksichtigen, die die Messergebnisse negativ beeinflussen können, wenn sie nicht angemessen angegangen werden.
TCLIB Suite trägt dazu bei, die Qualität des Systems zu verbessern, indem es die bestmöglichen Bilder für die von Ihnen gewählte Messsoftware liefert, wodurch wiederum die bestmöglichen Messergebnisse erzielt werden. In der Tat ist eine Kantenerkennungs-, Pattern-Matching- und Kalibriersoftware genauer und zuverlässiger, wenn sie auf gut ausgerichteten, homogen, von hinten beleuchteten, unverzeichneten Bildern basiert.
TCLIB APP ist eine full GenTL konforme Software. Jedes GenTL konformes Kameragerät kann mit dieser Software verwendet werden. Kamera Treiber von den Hersteller müssen auf jeden Fall installiert sein, damit das Programm korrekt laufen kann.
Learn
Online tools
Zur Tclib Suite Gehören:
- Spezielle Werkzeuge für die grundlegenden Einstellungen eines Messsystem: Ausrichtung des telezentrischen Objektivs und des kollimierten Lichtes, Ausrichtung der Objektebene, beste Fokussierung (TCLIB-APP).
- Ein Satz von Algorithmen (C++-Library) zur Berechnung des Verzeichnungsfeldes eines Systems und zur Korrektur aller neuen, vom System aufgenommenen Bilder (TCLIB) im Live-Modus, sowie alle in der TCLIB-APP entwickelten Funktionen.
Die eigenständigen Werkzeuge und die Funktionen für die Verzeichnungskalibrierung werden offline eingesetzt, wenn eine erste Optimierung und Kalibrierung der Maschine erforderlich ist. Die Verzeichnungskorrektur basiert dagegen auf schnellen und zuverlässigen Algorithmen, wodurch das System korrigierte Bilder im Live-Modus streamen kann.
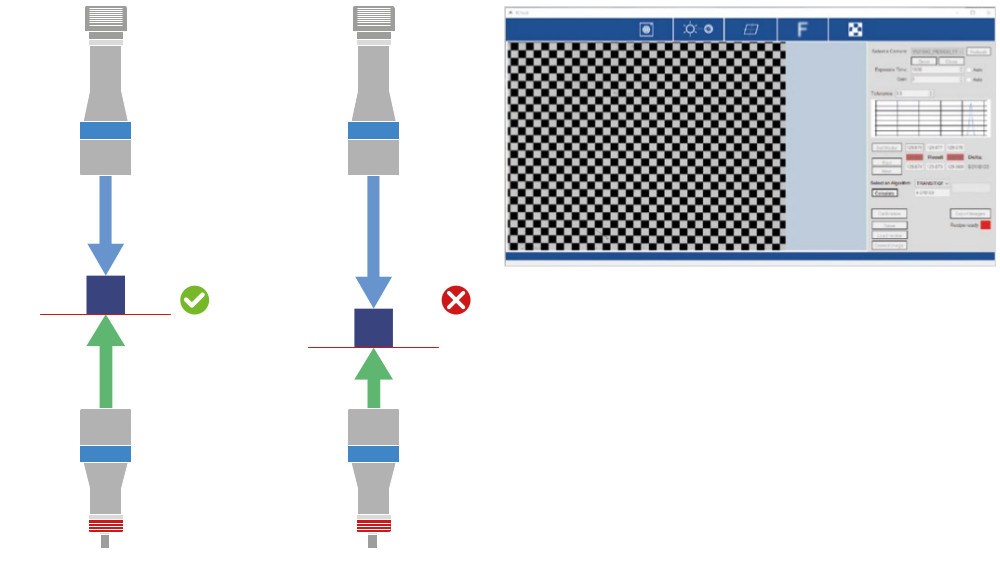
Ausrichtung des Objektivs und der Quelle des kollimierten Lichtes
Dieses Tool unterstützt den Bediener dabei, eine möglichst homogene Beleuchtung einzurichten.
Eine möglichst homogene Beleuchtung ist der erste grundlegende Schritt hin zu einem guten Messsystem, da sie sich auf die Zuverlässigkeit aller Algorithmen für die Kantenerkennung auswirkt.
Das Tool arbeitet im Live-Modus und gibt ein visuelles Feedback zur Ausrichtung. Das Sichtfeld (FOV) ist in ROIs eingeteilt, von denen jeder für die Ausrichtung über ein Farb-Feedback verfügt:
- ROT: nicht homogen
- GELB: einigermaßen homogen
- GRÜN: gute Homogenität
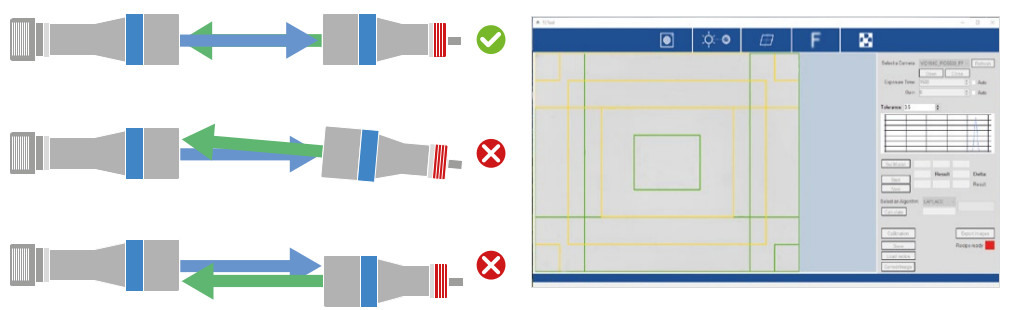
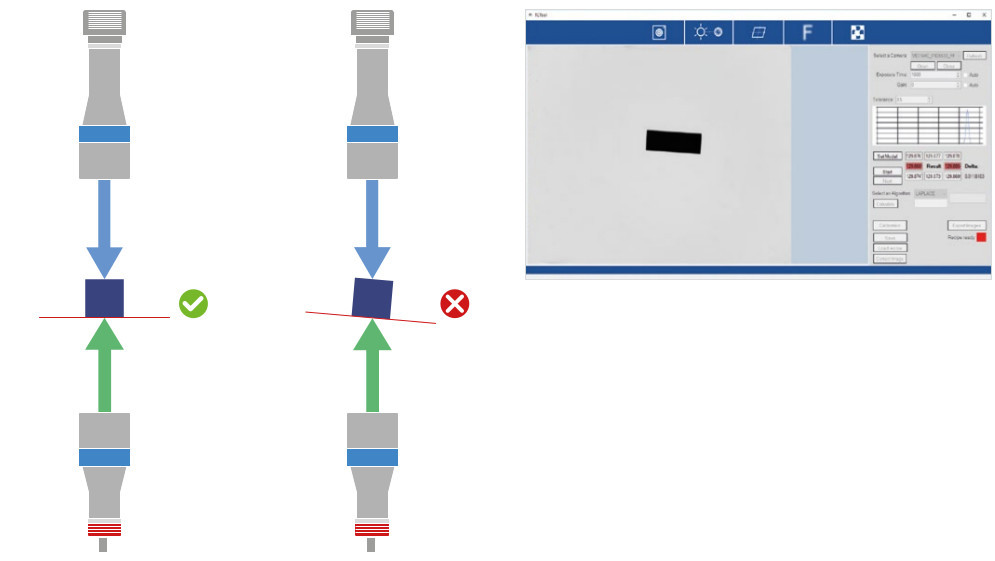
Ausrichten der Objektebene
Eine gute Ausrichtung der Objektebene an der optischen Achse ist essentiell. Folgen einer Fehlausrichtung:
- Mit einer Hintergrundbeleuchtung betrachten wir die Objektprojektion, nicht ihr tatsächliches Profil, daher kann das Bild durch einige Kompressionen in bestimmte Richtungen beeinflusst werden.
- Einige Merkmale befinden sich möglicherweise nicht gleichzeitig im besten Brennpunkt, was die Qualität der Kante bei der Vermessung beeinträchtigt.
Beste Konzentration
Dieses Tool liefert für jedes Bild einen numerischen Index, der angibt, wie dicht man am besten Brennpunkt ist
Verzeichnungskorrektur
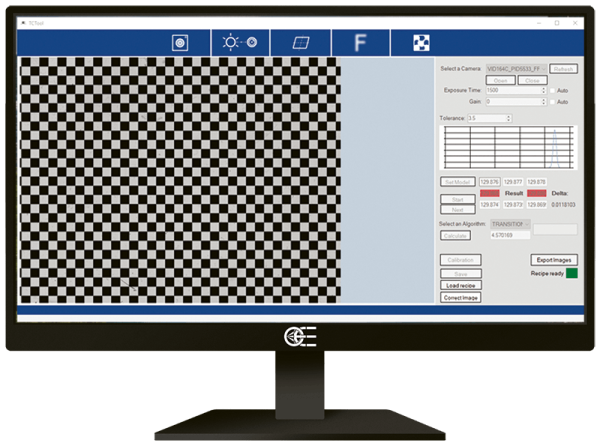
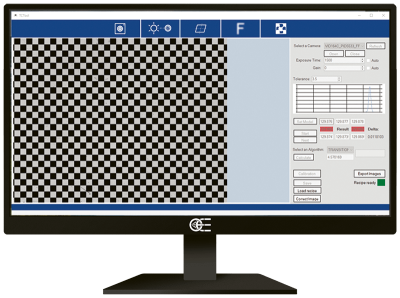
Mit diesem Tool kann die verbleibende, durch telezentrische Objektive bedingte, optische Verzeichnung eliminiert werden – so klein dieser Wert auch sein mag, er muss so nah wie möglich an Null liegen, um optimale Ergebnisse zu erzielen. Aus einem einzigen Bild eines Schachbrettmusters, das das gesamte Sichtfeld abdeckt (wie z.B. die PT-Serie von Opto Engineering®), erhalten wir alle Informationen, die notwendig sind, um die Verzeichnungen zu beseitigen.
Vorgehensweise:
- Ein einziges Bild des Kalibriermusters aufnehmen (offline)
- Anhand dieses Bildes wird ein Verzeichnungsfeld erstellt (offline)
- Das Verzeichnungsfeld wird in einer Referenzdatei gespeichert
- Durch Aufrufen des gespeicherten Verzeichnungsfeldes wird die Verzeichnung auf allen neu aufgenommenen Bildern beseitigt (online)
Schritt 1 und 2 entsprechen einer Kalibrierung des Systems und müssen folglich nur einmal durchgeführt werden. Schritt 4 wird für jede neue Aufnahme wiederholt.Alle diese Funktionen sind in die .dll-Datei der Library und in eine eigenständige Demo-Software integriert. Die Demo-Anwendung kann zu Testzwecken oder zum Abrufen des Verzeichnungsfeldes verwendet werden, während für die eigentliche Online-Korrektur die Integration der .dll-Datei empfohlen wird.
Ergebnisse eines optimieren telezentrischen systems
Um verschiedene Anordnungen möglicher telezentrischer Systeme zu optimieren, haben wir die Ergebnisse der Verwendung von TCLIB Suite überprüft. Die Ergebnisse betreffen die folgenden vier Tools der Suite:
- Die Ausrichtung des Linsenlichts entspricht der Homogenität der Beleuchtung (Standardabweichung des durchschnittlichen Graupegels).
- Die Ausrichtung der Linsenobjektebene entspricht dem niedrigsten erhaltenen Wert in Grad.
- Die Fokusgenauigkeit wird als die Empfindlichkeit in mm beim Arbeitsabstand angegeben und
- die Verzerrungskalibrierung als Wiederholbarkeit bei 20 Messungen eines 5-mm-Endmaßes
| TCCP3MHR144-C + LTCLCP144-G + PTCP-S1-HR1-C + ITA120-GM-10C | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sichtfeld | AUSRICHTUNG DES OBJEKTIVLICHTES als HINTERGRUND-HOMOGENEITÄT | AUSRICHTUNG DER OBKETEBENE als BESTER (ENGSTEN) WINKEL ZWISCHEN DEN EBENEN | BESTER FOKUS als BESTE (NIEDRIGSTE) UNSICHERHEIT AUF WD | VERZEICHNUNGSKALIBRIERUNG als ERGEBNIS VON 20 WIEDERHOLTEN MESSUNGEN | ||||||||||
| 164x120 mm | 4% | 0.012° | +/- 0.5 mm |
| ||||||||||
| TC3MHR144-C + LTCL144-G + PT120-240 (veraltet) + ITA120-GM-10C | ||||||||||||||
| Sichtfeld | AUSRICHTUNG DES OBJEKTIVLICHTES als HINTERGRUND-HOMOGENEITÄT | AUSRICHTUNG DER OBKETEBENE als BESTER (ENGSTEN) WINKEL ZWISCHEN DEN EBENEN | BESTER FOKUS als BESTE (NIEDRIGSTE) UNSICHERHEIT AUF WD | VERZEICHNUNGSKALIBRIERUNG als ERGEBNIS VON 20 WIEDERHOLTEN MESSUNGEN | ||||||||||
| 141x104 mm | 3% | 0.014° | +/- 0.5 mm |
| ||||||||||
| TC3MHR144-C + LTCL144-G + PTCP-S1-HR1-C + ITA120-GM-10C | ||||||||||||||
| Sichtfeld | AUSRICHTUNG DES OBJEKTIVLICHTES als HINTERGRUND-HOMOGENEITÄT | AUSRICHTUNG DER OBKETEBENE als BESTER (ENGSTEN) WINKEL ZWISCHEN DEN EBENEN | BESTER FOKUS als BESTE (NIEDRIGSTE) UNSICHERHEIT AUF WD | VERZEICHNUNGSKALIBRIERUNG als ERGEBNIS VON 20 WIEDERHOLTEN MESSUNGEN | ||||||||||
| 141x104 mm | 3% | 0.003° | +/- 0.5 mm |
| ||||||||||
| TCCR3M064-C + LTCLCR064-G + PT064-096 + ITA120-GM-10C | ||||||||||||||
| Sichtfeld | AUSRICHTUNG DES OBJEKTIVLICHTES als HINTERGRUND-HOMOGENEITÄT | AUSRICHTUNG DER OBKETEBENE als BESTER (ENGSTEN) WINKEL ZWISCHEN DEN EBENEN | BESTER FOKUS als BESTE (NIEDRIGSTE) UNSICHERHEIT AUF WD | VERZEICHNUNGSKALIBRIERUNG als ERGEBNIS VON 20 WIEDERHOLTEN MESSUNGEN | ||||||||||
| 62x46 mm | 3% | 0.001° | +/- 0.5 mm |
| ||||||||||
Was bedeutet Verzeichnungskalibrierung?
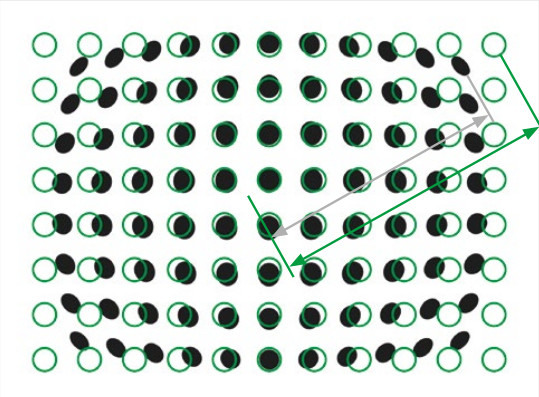
Immer, wenn wir ein optisches System verwenden, d. h. ein Objektiv und eine passende Kamera, müssen wir uns mit der sog. Verzeichnung auseinandersetzen. Die optische Verzeichnung des Systems kann als ein Hintergrundrauschen bezeichnet werden, das dazu führt, dass eine Reihe von Punkten nicht an der tatsächlichen Stelle, sondern an anderen Stellen abgebildet wird.
Ein typisches Beispiel ist eine gerade Linie, die aufgrund der Verzeichnung des Objektivs als Kurve abgebildet wird. Abb. 1 zeigt den Verzeichnungseffekt an einem Kalibrierpattern.
Die mathematische Transformation, die das ursprüngliche unverzeichnete Sichtfeld mit dem verzeichneten Bild verbindet, kann sehr schwer zu modellieren sein, v. a. wenn man bedenkt, dass sie sich durch das Sichtfeld selbst erheblich ändern kann.Die Verzeichnung wirkt sich auf die Messtechnik zunächst in Form eines Verlustes der Wiederholbarkeit der Messungen aus: Da ein Objektmerkmal je nachdem, wo sich das Objekt aufgrund der Verzeichnung im Sichtfeld befindet, etwas anders „aussieht“, wird sich der Wert einer Messung an diesem Merkmal wahrscheinlich jedes Mal ändern, wenn das Objekt entfernt und wieder zurückgestellt wird.
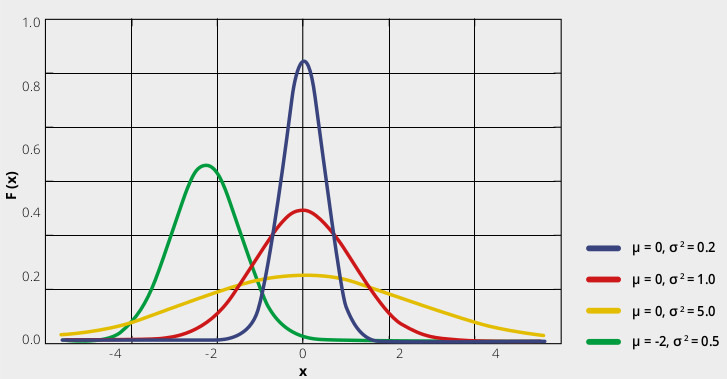
Wiederholbarkeit eines Messsystems
Wenn wir den Durchmesser eines durchgehenden Lochs 100 Mal messen, kann die Verteilung der Ergebnisse durch eine Gauß-Kurve ungefähr bestimmt werden: Dem Durchschnitt nahe liegende Ergebnisse sind sehr häufig, während Ergebnisse mit großen Abweichungen davon unwahrscheinlich sind. Die Wiederholbarkeit der Messung steht mit der Breite der Glocke in Zusammenhang: Je schmaler die Glocke ist, desto schwieriger wird es sein, einen Messwert zu finden, der weit vom Durchschnitt entfernt liegt. In anderen Wort ist eine Funktion (z. B. eine Länge) „fast immer fast gleich“. Andererseits bedeutet eine breite Glocke, dass wir nicht sagen können, ob ein Maß tatsächlich vom erwarteten Wert abweicht (z.B. weil es ein defektes Teil ist) oder ob es sich um einen statistisch erwarteten Ausreißer handelt, der durch die geringe Wiederholbarkeit unseres Messsystems bedingt ist.Die in der Regel verwendete Breite wird Sigma (oder „Halbwertsbreite“ (FWHM)) genannt und steht in direktem Zusammenhang mit der Wiederholbarkeit. Deshalb kann eine direkte Methode zum Abgleich der Genauigkeitsanforderungen festgelegt werden: Wenn die Toleranz einer Messung als Vielfaches ihres spezifischen Sigma-Wertes angegeben wird, bestimmen wir daraus folgend die Wahrscheinlichkeit, mit der ein Teil außerhalb des Toleranzbereichs liegt. Ein Gegenstand mit einer Übereinstimmung von zwei Sigma befindet sich demnach in 95 % der Male innerhalb des Toleranzbereichs. Ein Gegenstand mit drei Sigma verfügt über eine statistische Sicherheit von 99,7 %, die bei 5 Sigma auf 99.99999 % ansteigt.Angenommen, Ihre Verteilung hat einen Durchschnittswert von 150 mm und Sigma beträgt 1 mm. Der zugehörige Fehler hängt vom Vertrauenswert für Ihre Anwendung ab. In der Tat können wir in den Angaben feststellen, dass seine Länge 150 mm +/- 3 mm beträgt, was in 99,7% der Fälle dann auch der Fall sein wird. Wenn wir andererseits wollen, dass 1 mm einer 3-Sigma-Toleranz entspricht, müssen wir unseren Messprozess auf 1 Sigma = 0,33 mm verbessern.