Tutorial: Objektive der Telezentrie
Grundlagen und Funktionsprinzipien der Telezentrie
Bi-telecentric lenses tutorial
In den letzten Jahren ist die Verwendung von Technologien der industriellen Bildverarbeitung für die dimensionale Messung sehr beliebt geworden. Die Verbesserung von Kameras, Softwares und Beleuchtungskomponenten ermöglichen eine Genauigkeit, die manchmal nicht einmal von kontakt- oder laserbasierenden Methoden übertroffen wird.
Erfolgreiche Integratoren der industriellen Bildverarbeitung sind sich zunehmend bewusst, dass Qualitätsoptik überlegene Systemleistungen erzeugt und dass telezentrische Objektive für jede Bildgebungsanwendung für die Dimensionsmessung notwendig sind. Softwareentwickler, die auf die Präzisionsmessung mechanischer Teile angewiesen sind, benötigen kontrastreiche Bilder mit möglichst geringer geometrischer Verzeichnung. Perspektivische Effekte, die eine Veränderung der Vergrößerung bewirken, wenn das Objekt nicht präzise positioniert oder stark dreidimensional ist, sind ebenso zu minimieren oder zu beseitigen.
Außer den Problemen der Bildverarbeitung müssen die Entwickler von Bildverarbeitungssystemen zudem berücksichtigen, dass herkömmliche entozentrische Optiken verschieden Faktoren beinhalten, die die Genauigkeit und Wiederholbarkeit von Messanwendungen begrenzen:
- Veränderung der Vergrößerung, verursacht durch Objektverschiebung
- Bildverzeichnung
- Perspektivische Fehler
- Schlechte Bildauflösung
- Unsichere Lokalisierung der Objektränder, verursacht durch Lichtgeometrie
Telezentrische Objektive reduzieren oder beseitigen die meisten dieser Probleme und sind daher für die Entwicklung von Messanwendungen höchster Präzision unverzichtbar geworden.
Grundlegende Objektivtypen
Konstante Vergrösserung
Bei Messanwendungen wird häufig eine orthonormale Ansicht des Objektes benötigt (d.h. die Objektseiten werden nicht abgebildet), damit korrekte lineare Messungen durchgeführt werden können. Zudem können viele mechanische Teile nicht präzise positioniert werden (z.B. aufgrund von Vibrationen) oder die Messung muss in verschiedenen Tiefen durchgeführt werden oder, schlimmer noch, die Objektdicke (und damit die Position der Objektoberfläche) kann unterschiedlich sein; dennoch benötigen Softwareentwickler eine perfekte Korrelation zwischen abgebildeten und realen Dimensionen.
Herkömmliche Objektive liefern verschiedene Vergrößerungen bei verschiedenen Konjuganten: In der Folge verändert sich die Größe der Abbildung beim Verschieben des Objekts fast proportional mit dem Abstand des Objektes zum Objektiv. Dies kann man auch im Alltag feststellen, wenn man Bilder mit einer Kamera mit einem Standard-Fotoobjektiv aufnimmt.
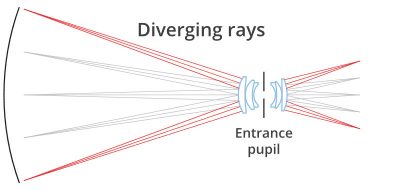
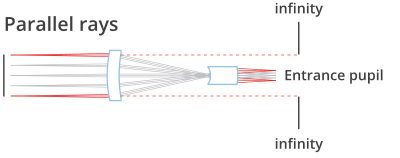
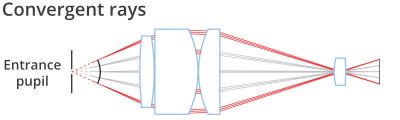
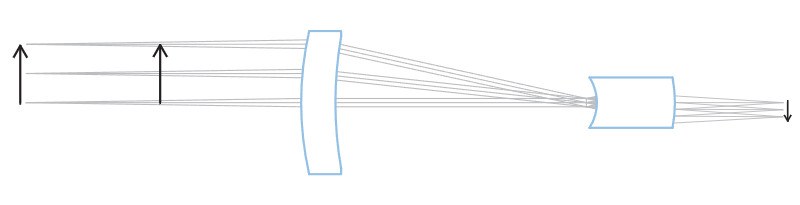
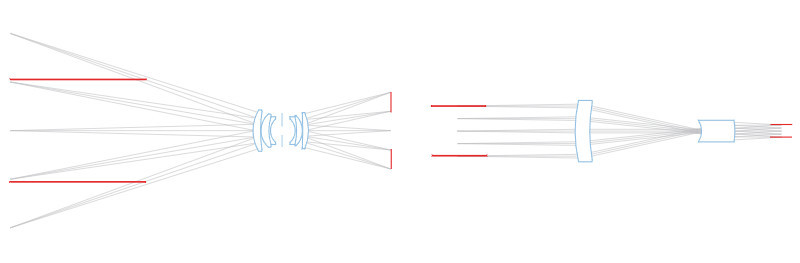
Bei telezentrischen Objektiven bleibt die Bildgröße bei Verschiebung des Objektes nahezu unverändert, vorausgesetzt das zu inspizierende Objekt befindet sich innerhalb des vorgegebenen Bereichs, der oft als "Schärfentiefe" oder "telezentrischer Bereich" genannt wird. Dies ist auf den besonderen Strahlengang innerhalb des optischen Systems zurückzuführen: Das Objektiv sammelt vom abzubildenden Objekt nur Strahlenbündel, deren barizentrischer Strahl (oder Hauptstrahl) parallel zur optomechanischen Hauptachse verläuft. Aus diesem Grund ist der Durchmesser der vorderen Linse mindestens so groß wie die Diagonale des Objektfeldes.
Dies wird ermöglicht, indem die Blendenöffnung exakt im Brennpunkt der Frontgruppe platziert wird: Die einfallenden Strahlen treffen auf die Eintrittspupille, die so erscheint, als sei sie virtuell im Unendlichen platziert. Der Begriff "telezentrisch" setzt sich zusammen aus den Wörtern "tele" (aus dem Griechischen, bedeutet entfernt) und "Zentrum", was für Blendenöffnung steht, dem tatsächlichen Zentrum des optischen Systems.
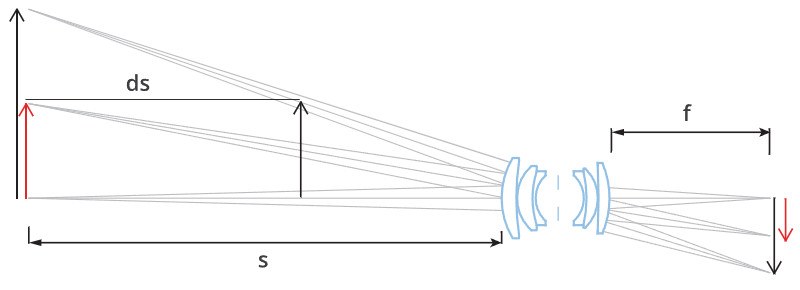
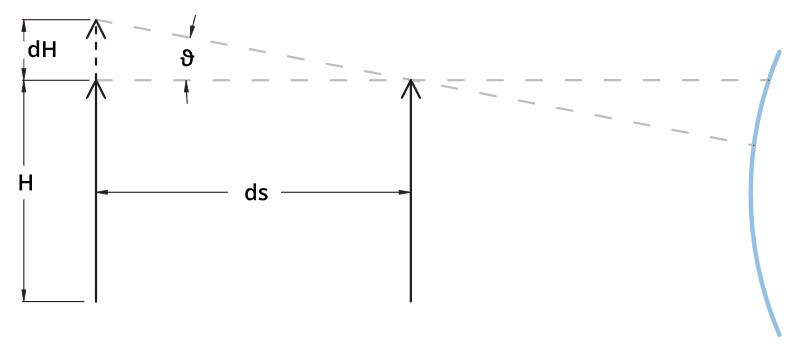
Um ein Gefühl für den Unterschied zwischen den beiden Objektivtypen zu bekommen, stellen wir uns z.B. ein gewöhnliches Objektiv mit einer Brennweite f = 12 mm vor, angeschlossen an einen 1/3" Detektor, ausgerichtet auf ein Objekt von einer Höhe H = 20mm bei einer Entfernung s = 200 mm. Nehmen wir an, dass das Objekt von seiner Ausgangsposition um ds = 1 mm verschoben wird, so scheint sich seine Größe wie folgt zu ändern:
dH = (ds/s) · H = (1/200) · 20 mm = 0,1 mm
Bei einem telezentrischen Objektiv hängt die Veränderung der Vergrößerung von der telezentrischen Neigung ab: Gute telezentrische Objektive weisen eine effektive telezentrische Neigung Theta von ca. 0.1° (0,00117 rad) auf; das bedeutet, dass sich die Größe des Objektes um nur 0,0017 mm für jede Verschiebung ds von 1 mm ändert:
dH = ds · theta= 1 · 0,0017 mm = 0,0017 mm
Daher beträgt bei telezentrischen Objektiven der Vergrößerungsfehler 1/10 bis 1/100 im Vergleich mit gewöhnlichen Objektiven.
Das Konzept "Telezentriebereich" oder "telezentrische Tiefe" wird oft als Schärfentiefenbereich interpretiert, wo die Vergrößerung konstant bleibt. Das ist eine irreführende Auslegung, da sie impliziert, dass der verbleibende Platz "nicht-telezentrisch" ist. Doch dieser Parameter sollte immer mit dem maximalen, durch die Linse verursachten Messfehler innerhalb desselben Bereichs assoziiert werden. Ein viel wichtigerer Parameter ist die "telezentrische Neigung" (oben als "Theta" bezeichnet) oder die "Telezentrie". Ein solcher Winkel definiert den Messfehler durch die Verschiebung eines Objekts, egal wo sich das Objekt befindet: Die Höhe der Fehler ist offensichtlich raum-unabhängig, weil die optischen Hauptstrahlen "gerade verlaufen".
Um die eintretenden telezentrischen Strahlen einzufangen, muss die Frontlinse eines telezentrischen Objektivs mindestens so groß wie die maximale Größe des Objektes sein. Aus diesem Grund sind telezentrische Objektive größer, schwerer und somit auch teurer als herkömmliche Objektive.
Geringe Verzeichnung
Verzeichnung ist eines der schwerwiegendsten Probleme, die die Messpräzision einschränken. Alle Objektive weisen zumindest eine geringe Verzeichnung auf und oft ist sogar ein einziges Pixel Differenz zwischen dem realen Bild und dem erwarteten Bild kritisch.
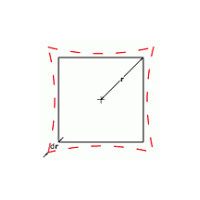
Verzeichnung wird ganz einfach definiert als die prozentuale Differenz zwischen der Distanz eines Bildpunktes von der Bildmitte und der gleichen Distanz in einer verzeichnungsfreien Abbildung; anders gesagt, die Abweichung der abgebildeten von der tatsächlichen Größe des Objekts. Hat beispielsweise die Ecke der Abbildung eines Quadrates einen Abstand zur Bildmitte von 198 Pixeln, während der Abstand ohne Verzeichnung 200 Pixel betragen würde, so beträgt die radiale Verzeichnung an diesem Punkt:
Verzeichnung = (198 - 200) / 200 = -2/200 = 1%
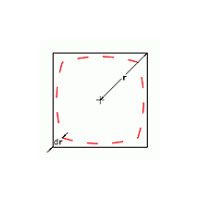
Positive radiale Verzeichnung wird kissenförmige, negative radiale Verzeichnung tonnenförmige Verzeichnung genannt. Verzeichnung kann auch als eine geometrische Transformation des dreidimensionalen Raums der realen Welt in den virtuellen, vom Objektiv geschaffenen zweidimensionalen Raum des Abbildes angesehen werden: Da diese Transformation nicht perfekt linear ist, sondern sich Polynomen zweiten oder dritten Grades annähert, wird das Bild leicht gestreckt oder deformiert.
Gewöhnliche Optiken weisen Verzeichnungswerte auf, die von wenigen Prozenten bis zu einigen 10 Prozenten reichen und somit präzise Messungen sehr schwierig gestalten. Die Korrektur der Verzeichnung wird sogar noch komplizierter, wenn nicht-telezentrische Objektive verwendet werden. Die Existenz der Verzeichnung beruht darauf, dass das menschliche Auge eine Verzeichnung von 1- 2% leicht kompensiert, und da die meisten in der industriellen Bildverarbeitung verwendeten Optiken für Videoüberwachung oder Fotografie entwickelt wurden, kam es darauf nicht an. In einigen Fällen, wie bei Fish-Eye-Objektiven oder Objektiven für Webcams, wird die Verzeichnung eigens herbeigeführt, damit das Objektiv mit weitem Winkel arbeiten und eine gleichmäßige Beleuchtung des Detektors garantiert werden kann (in diesen Fällen hilf die Verzeichnung auch dabei, die Effekte des Kosinus-hoch-vier-Gesetzes zu reduzieren).
Telezentrische Objektive weisen normalerweise einen sehr geringen Verzeichnungsgrad auf, d.h. rund 0,1%: Das bedeutet, das der größtmögliche Verzeichnungsfehler geringer als 1 Pixel einer hochauflösenden Kamera sein sollte.
Daher muss in den meisten Anwendungen die Verzeichnung durch eine Software ausgeglichen werden: Ein präzises Pattern (dessen geometrische Ungenauigkeit weniger als 10% der benötigten Messgenauigkeit sein sollte) muss in der Mitte der Schärfentiefe positioniert werden; dann ist die Verzeichnung in verschiedenen Bildpunkten zu errechnen und der Algorithmus der Software interpretiert das Ursprungsbild und wandelt es in ein verzeichnungsfreies Bild um.
Nur wenige wissen, dass die Verzeichnung auch vom Objektabstand abhängt und nicht nur von der Optik selbst. Aus diesem Grund ist es sehr wichtig, dass der nominale Arbeitsabstand beibehalten wird.
Um nicht-achsialsymmetrische Verzeichnung zu vermeiden muss sehr sorgfältig darauf geachtet werden, dass Objektiv und zu inspizierendes Objekt genau rechtwinklig zueinander ausgerichtet sind. Trapezoidale Verzeichnung (besser bekannt als "Keystone"- oder "Thin Prism"-Effekt) ist ebenfalls ein wichtiger Parameter, welcher bei einem Objektiv zu minimieren ist, da er asymmetrisch ist und sehr schwierig durch Software ausgeglichen werden kann. Mechanismen für die Objektivfokussierung können auch eine gewisse symmetrische oder nicht-symmetrische Verzeichnung aufgrund mechanischen Spiels oder Dezentrierung von optischen Elementen bewirken.
Begrenzung perspektivischer Fehler
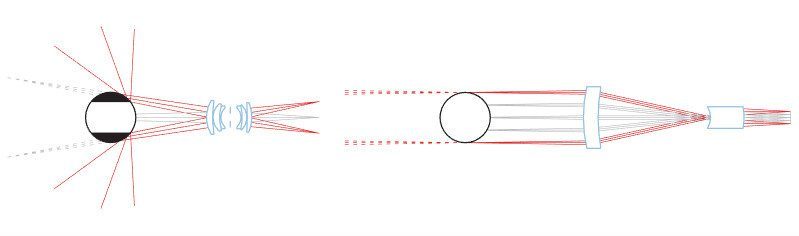
Wenn für die Abbildung dreidimensionaler Objekte (nicht vollständig flache Objekte) herkömmliche Objektive verwendet werden, sind die Bilder entfernter Objekte kleiner als diejenigen naher Objekte. Wird ein Objekt wie z.B. eine zylindrische Höhlung abgebildet, erscheinen folglich die kreisförmigen Ränder oben und unten konzentrisch, obwohl beide Kreise perfekt identisch sind.
Bei Verwendung eines telezentrischen Objektives hingegen verschwindet der untere Rand, da er vom oberen kreisförmigen Rand verdeckt wird.
Dieser Effekt wird durch den spezifischen Strahlengang hervorgerufen: Im Falle herkömmlicher Optik zeigt jede zur optischen Hauptachse parallele geometrische Information eine Komponente auf der Detektorebenenrichtung, während bei einem telezentrischen Objektiv diese rechtwinklige Komponente überhaupt nicht vorhanden ist.
Es ist als ob herkömmliche Objektive eine Übereinstimmung zwischen der dreidimensionalen Objektwelt und des zweidimensionalen Detektor- (Bild-)raums schaffen würden: Mit einem telezentrischen Objektivs wird die dritte Dimension im Objektraum nicht dargestellt, was bedeutet, dass diese sich perfekt für Querschnitt-Abbildungen und Messungen eignen.
Gute Bildauflösung
Die Bildauflösung wird als CTF (contrast transfer function) erfasst, ein Parameter, der das Kontrastverhältnis bei einer vorgegebenen räumlichen Frequenz auf der Kameradetektorfläche beschreibt, ausgedrückt in lp/mm (Linienpaare pro Millimeter).
Unerfahrene Integratoren verwenden häufig Kameras mit einer großen Anzahl kleiner Pixel kombiniert mit billigen Objektiven mit geringer Auflösung, was zu einem unscharfen Bild führt. Die Auflösung telezentrischer Objektive ist sogar mit der kleinsten Pixelgröße und Kameras mit hoher Auflösung kompatibel, wodurch die Messauflösung erhöht wird.
Keine Unsicherheit bei der Lokalisierung der Ränder
Oft wird durch die Hintergrundbeleuchtung die genaue Lokalisierung der Objektränder erschwert.
Das kann passieren, wenn das Signal der hellen Pixel des Hintergrundes von jenem der dunklen Pixel der Objektränder überlappt wird. Wenn das Objekt stark dreidimensional ist, kann ein weiterer Effekt die Messgenauigkeit stark beeinträchtigen: Wie in der folgenden Abbildung gezeigt wird, können die von den Randzonen des Objektes nahe der Objektränder kommenden Strahlen vom Objekt selbst reflektiert werden.
Sie werden vom Objektiv als direkt von der Rückseite des Objektes kommende Strahlen interpretiert. Das bedeutet, dass einige marginale Teile des Objektes verschwinden können und somit die Messung sehr unpräzise und instabil werden lassen.
Dieser Effekt kann wirkungsvoll durch die Verwendung eines telezentrischen Objektivs vermindert werden, da bei ausreichend kleiner Blendenöffnung nur die Strahlen von der Objektoberfläche reflektiert werden und in die Optik eindringen können, die parallel oder beinahe parallel zur optischen Hauptachse verlaufen.
Da diese Strahlen nur sehr geringen Abweichungen unterworfen sind, beeinflusst die Reflektion auf der Objektoberfläche die Messgenauigkeit nicht so sehr.
Um dieses Problem vollständig zu vermeiden, können kollimierte (oft auch „telezentrisch“ genannte) Beleuchtungen an telezentrische Objektive angeschlossen werden, die zu Objektivöffnung und Bildbereich passen müssen. Bei dieser Lösung wird das gesamte vom Beleuchter ausgehende Licht vom Objektiv gesammelt und an den Detektor übergeben und ermöglicht somit extrem hohe Signal-Rausch-Verhältnisse und unglaublich kurze Belichtungszeiten. Gleichzeitig treten nur die gewünschten Strahlen in das abbildende Objektiv ein und es gibt keine Probleme an den Rändern.
Vorteile von bi-telezentrisschen Objektiven
1. Bessere Vergrösserungskonstanz
Herkömmliche Optiken und normale telezentrische Objektive neigen zu einem schlechten Verhalten, da die Strahlenbündel je nach Feldposition verschiedene Neigungen haben und das optische System ebenfalls nicht symmetrisch ist. Außerdem ist die optische Wellenfront vollkommen asymmetrisch, da einfallende telezentrische Strahlen im Bildraum nicht-telezentrisch werden. Folglich hat der vom Interzeptor zwischen dem Strahlenbündel und der Detektorebene erzeugte Spot im Bildzentrum eine andere Form und Grösse als an den Bildrändern (die Punktstreuungsfunktion variiert und wird unsymmetrisch; der Spot wird breiter und ellyptisch).
Zusätzlich bewegt sich der von Puntkstrahlen erzeugte Spot über die Bildebene vor und zurück wenn das Objekt in der Schärfentiefe verschoben wird, was eine kleine Änderung der Vergrößerung bewirkt, die für strenge Präzisionsmessungen nicht zulässig ist. Aus diesem Grund weisen nicht bi-telezentrische Objektive eine geringere Vergrößerungskonstanz auf, auch wenn ihre nur im Objektbereich gemessene Telezentrie sehr gut sein kann.
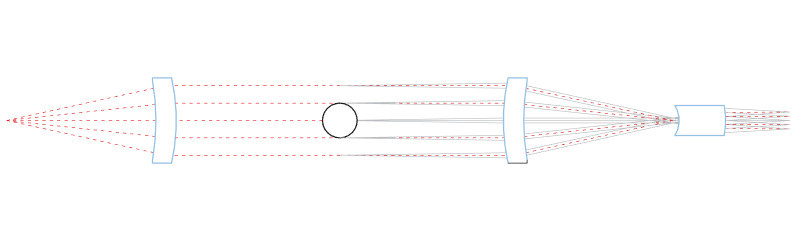
Bi-telezentrische Objektive sind sowohl im Objekt- als im Bildraum telezentrisch, was bedeutet, dass Hauptstrahlen nicht nur beim Eintreten in das Objektiv sondern auch beim Austreten aus dem Objektiv parallel sind.
Diese Eigenschaft ist wesentlich bei der Behebung von Problemen mit der Genauigkeit. Probleme, die mit mono-telezentrischen Objektiven wie Inhomogenität der Punktstreuungsfunktion und mangelnder Vergrößerungskonstanz durch die Schärfentiefe zusammenhängen.
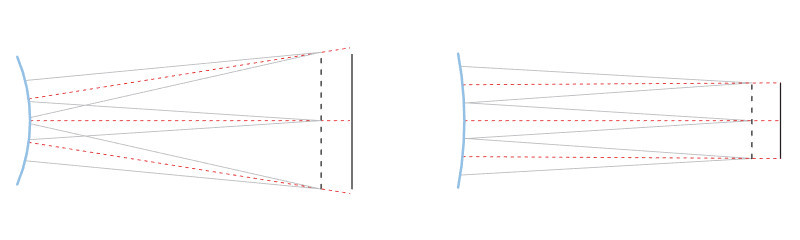
2. Erhöhte Schärfentiefe
Die Schärfentiefe ist die maximal von der besten Brennpunktsituation akzeptierte Ausgangsposition des Objektes. Jenseits dieser Grenze wird die Bildauflösung nicht mehr akzeptiert, da die von einem Objektpunkt ausgehenden Strahlen nicht in einem ausreichend kleinen „Spot“ auf die Detektoroberfläche treffen: Mehrere Pixel tragen Informationen von dem selben Objekt (Unschärfe) und die Fokussierung wird schlecht. Die Schärfentiefe hängt im Wesentlichen von der Blendenzahl der Optik ab: Je größer die Blendenzahl (d.h. je kleiner die Blendenöffnung der Optik) desto größer die Schärfentiefe, mit einer fast linearen Abhängigkeit. Durch Schließung des Objektivdiaphragmas, was eine Erhöhung der Blendenzahl bedeutet, wird die Divergenz des Strahlenbündels verringert; die Streuung der Strahlen wird dadurch geringer und ermöglicht somit eine geringere Größe des Spots auf dem Detektor. Jenseits einer bestimmten Blendenzahl wird die Auflösung schlechter statt besser; Grund dafür sind Brechungseffekte, die die minimale Blendenöffnungsgröße begrenzen, wenn ein kontrastreiches Bild benötigt wird.
Bildseitige Telezentrie oder Bi-Telezentrie zeichnet sich durch die Beibehaltung eines sehr guten Bildkontrastes aus, sogar wenn sehr dicke Objekte betrachtet werden; Grund dafür ist die Symmetrie des optischen Systems, die die Beibehaltung der Symmetrie der Strahlenspots und als Konsequenz der Unschärfe vereinfacht. Das resultiert in einer Schärfentiefe, die als 20-30% größer als diejenige nicht bi-telezentrischer Optiken wahrgenommen wird.
3. Gleichmässige Detektorbeleuchtung
Die mithilfe von Bi-Telezentrie erreichte gleichmäßige Beleuchtung des Detektors ist für verschiedene Anwendungen wie LCD-, Textil- und Druckqualitätskontrolle nützlich.
Wenn dichroitische Filter für photometrische oder radiometrische Messungen in den Strahlengang integriert werden müssen, garantiert die Bi-Telezentrie, dass die Achse des Strahlenfächers die Filternormale trifft und seine Oberfläche den optischen Bandpass über die gesamte Oberfläche des Kameradetektors beibehält.

Wann telezentrische Objektive verwendet werden sollten
- When a thick object (thickness > 1/10 FOV diagonal) must be measured
- When different measurements on different object planes must be carried out
- When the object-to-lens distance is not exactly known or cannot be predicted
- When holes must be inspected or measured
- When the profile of a piece must be extracted
- When the image brightness must be very even
- When a directional illumination and a directional “point of view” are required.